
做自己论坛--给现实加点理想我们正式开始,今天我们的话题是《给现实加点理想》。我经常自许为一个现实的理想主义者,但是在中国做理想主义者是蛮悲催的事情。我觉得中国就是一个现实主义的集团,大部分人在这样一...
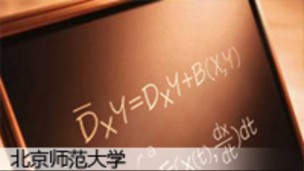
微分几何是研究一般的曲线和曲面在“小范围”上的性质的数学分支学科。微分几何和几何分析为学习广义相对论提供方法以及正确的框架,而广义相对论激发富有挑战性的各种问题。...

风水学,本为相地之术,即临场校察地理的方法,叫地相、中国古代称堪舆术,目的是用来选择宫殿、村落选址、墓地建设等方法及原则。原意是选择合适的地方的一门学问。...

数学与魔术,一个看似奇怪的组合。事实上,当今很多强大的魔术表演背后都少不了数学的支撑,可以说,数学在魔术效果中起着非常核心的作用。这一点毫不奇怪,如今我们使用的技术、购买的产品、所做的工作都离不开数学...

The Fourier transform is ubiquitous in engineering and science and this course is appropriate for st...

化学是医学和生命科学的重要理论基础和工具箱。化学原理更重要。本课程针对化学、生物、医学类的专业需求和学生的兴趣特点,来讲解重要的化学原理和化学理论。...

社会认知心理学是一门新的学科,它以信息加工理论和新颖巧妙的研究方法,把心理学的研究推进到一个崭新的阶段,成为当代心理学的主流和方向。本课程阐述了社会认知心理学的基本理论,介绍了社会认知心理学研究的最新...
它的研究对象是向量,向量空间。线性变换和有限维的线性方程组。本课程讲述了矩阵理论及线性代数的基本知识,侧重于那些与其他学科相关的内容,包括方程组、向量空间、行列式、特征值、相似矩阵及正定矩阵。...

本课程为微积分基础课程,内容涵盖单变量函数的微分、积分及应用。修这门课不需要任何的大学基础,只需要高中知识即可。微积分的目的无非是求小尺度的微分和大尺度的积分,它们之间通过微积分基本定理联系起来。...

微分方程论是数学的重要分支之一。大致和微积分同时产生,并随实际需要而发展。含自变量、未知函数和它的微商(或偏微商)的方程称为常(或偏)微分方程。它的研究来源极广,历史久远。...

朗读作为口语艺术,技巧性很强。要使朗读获得生动感人的效果,就必须掌握一定的朗读技巧。课程介绍了情感、声音和形体等各方面的技巧。天天快乐小镇...

东汉末年,三国纷争。公元220年曹丕篡汉,自此拉开了魏晋南北朝的序幕,公元420年刘裕代晋,开始更为混乱的政权争夺。政权更迭频繁的同时,却也加速了各地区文化的交流。各学派思想彼此渗透,文人雅士亦如雨后...

本课程内容包括向量和多变量微积分,属于是一年级第二学期微积分课程是麻省理工学院所有本科生必修科目。 主题包括向量和矩阵,偏导数,双重和三重积分,平面和空间微积分。麻省理工学院开放式课程提供了另外200...

有言有默。 该你说话的时候一句都不能少,不该说的时候,一句都不能多。 沟通如果只分出是非,那结果一定是伤感情的。但如果沟通没有得出是非,那就没有效果。最好是在圆满中分出是非。大家都有面子才叫圆满。...

领导力并不是技术和方法,更多的是来自一颗宽容的心。领导力是一种鼓舞人心的力量,无论是对自己亦或他人,伟大的领导力是关于人类的经验,而非过程。领导力并非规则或计划,它是来自内心和尊重他人内心的人类活动,...

企业创新需要很多条件,如人才、资金、技术与合理的创新管理体系等,但最关键的是具备一个创新的企业文化。但到底什么是创新的企业文化。...

这是为没有代数基础的学生准备的代数课程,包含方程及求解、不等式求解、作图、百分比、比值问题、因式分解、虚数和复数、二次方程、二次不等式、函数、对数及运算、圆锥曲线的坐标运算(椭圆、双曲线、抛物线)、分...