笔记-线性代数 - 好知网-重拾学习乐趣-Powered By Howzhi

同学笔记最热最新

线性代数10-施光燕教授的笔记

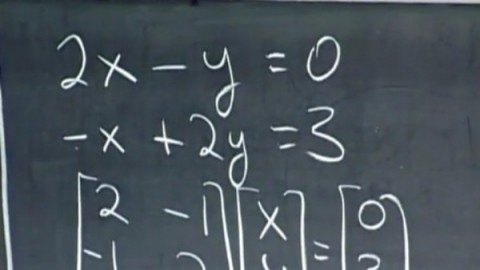
一、相似矩阵本讲所讲的均为方阵。A-方阵，P为同一阶的可逆方阵，A通过相似变换P<-1>AP=B,称A和B相似，记为A~B。定理，若A和B相似，则A,B具有相同的特征方程，也即有相同的特征值。二、矩阵的对角化A~λ（对角阵）结论：若A=PλP<-1>,则λ中对角元素λi必为A得特征值，P中得列向量pi必为A相应于λi的特征向量，反之亦然。结论：对称阵一定可以对角化。

by 一万年太久只争朝夕 0 0
线性代数09-施光燕教授的笔记

矩阵的特征值和特征向量和秩一样，是矩阵另外一个特征，但是针对于方阵。概念：对于方阵A，若有非零向量X和数λ使得AX=λX，则称数λ为A的特征值，称非零向量X为A相应于特征值λ的特征向量。结论 A-nxm设λ1，λ2，…λn为A的特征值，则λ1+λ2+…+λn=A的迹（矩阵的对角线元素之和叫做矩阵的迹）λ1λ2…λn=lAl相当于解一元二次方程得韦达定理。求法：1、lA-λil=0(i为单位阵)，解出λ，即为矩阵A的特征值。2、求齐次线性方程组(A-λi)x=0的基础解系，即为特征向量。

by 一万年太久只争朝夕 0 0
线性代数08-施光燕教授的笔记

线性方程组（三）线性方程组的理论，AX=B,(B≠0)为非齐次线性方程组，r(A)=r([AB])<n，n-r(A)个自由变量。解的性质1、若Y为AX=B的解，X是AX=0的解，则Y+X亦为AX=B的解。2、若Y1、Y2均为AX=B的解，则Y1-Y2亦为AX=0的解。齐次通解：对于AX=B，若AX=B的一个解Y和AX=0的基础解系X1,X2,…，Xk，k=n-r(A)，则AX=B的所有解即为X=Y+c1X1+c2X2+…+ckXk(其中c1,c2,…，ck为任意常数)步骤1、[A,B]转换为阶梯阵。2、确定自由变量。3、令所有自由变量为0，求得AX=B的一个特解Y。4、求出AX=0的基础解系。5、求通解。

by 一万年太久只争朝夕 0 0
线性代数07-施光燕教授的笔记

线性方程组（二）若有解，解是否是唯一的？r(A)=r([AB])=n 等价于解唯一；r(A)=r([AB])<n 等价于解不唯一；且有n-r(A)个自由变量。有解，不唯一，怎么掌握全体？AX=O齐次线性方程组A-mxn，r(A)<n有n-r(A)个自由变量。若X1,X2均为AX=O的解，则C1X1+C2X2(C1、C2为任意常数)也是AX=O的解，{XlAX=O}（注意这是一个集合）中极大无关组，又称AX=O的基础解系。求AX=O齐次方程组的通解的步骤：1、化为阶梯阵。2、确定n-r(A)个自由变量。3、令一个自由变量为1，其它为0，用遍这样的办法，得到n-r（A）组解，即构成基础解析。4、基础解系中的解分别乘上任意常数相加，即得通解。

by 一万年太久只争朝夕 0 0
线性代数06-施光燕教授的笔记

线性方程组（一）一、线性方程组的表达线性方程组可用增广阵表达，也可用线性方程的系数矩阵必达。一般地，AX=B, A-mxn,B-mx1A-系数阵 [AB]增广阵二、线性方程组的解法写出增广阵，初等行变换，阶梯阵，从最后一个非零行开始，得到方程的一般解，相当于精简方程组。齐次线性方程组（等号后面是0）和非其次线性方程组（等号后面不是0）。三、线性方程组的理论AX=B有解等价推出 r(A)=r（[AB]）系数矩阵的秩等于增广阵的秩。齐次线性方程组肯定是有解的。

by 一万年太久只争朝夕 0 0
线性代数05-施光燕教授的笔记

1、n维向量有序的若干个数称为向量。如四维向量，一般竖着排。向量实际是一个列矩阵。2、向量组的线性相关性称3α1+4α2-α3为α1，α2，α3的线性组合。若β=λ1α1+λ2α2+λ3α3，称β可用α1，α2，α3线性表出。关于向量组{α1，α2，…，αk}，若存在一组不全为0的数λ1，λ2，…，λk使 λ1α1+λ2α2+…+λkαk=O，则称向量组{α1，α2，…，αk}是线性相关的，否则称为线性无关的。考虑向量组的线性相关性等价于考虑相应的线性方程组是否非零解。3、极大线性无关组考虑向量组{α1，α2，…，αk}，希望以其它最少的部分去掌握全体，这最少的部分应满足：1）这部分是线性无关的；2）这组中每个向量都能用这部分线性表出。极大无关组不一定是唯一的，但极大无关组中向量个数是一定的。向量组的秩=极大无关组中向量的个数。{α1，α2，…，αk}推出[α1，α2，…，αk],通过初等行变换变为阶梯阵，若阶梯阵非零行的行数<向量个数，则向量组线性相关；若阶梯阵非零行的行数=向量个数，则向量组线性无关。向量组的秩=矩阵的秩

by 一万年太久只争朝夕 0 0
线性代数04-施光燕教授的笔记

初等行变换1、两行交换。2、某行乘非零常数。3、某行乘一常数加到另一行。初等行变换求逆。矩阵的秩（矩阵的其中一个特征）矩阵的子式（例如二阶子式，位于所取得交叉点上的元素构成）。矩阵A中非零子式的最高阶数称为A的秩，记为r(A)，秩为一个数，例如r(A)=3。A-mxn，r(A)≤m，r(A)≤n。n阶方阵A可逆，互推lAl≠0，互推r(A)=n，此为满秩。阶梯阵，结论：一个阶梯阵的秩等于非零行的行数。利用初等变换求秩，初等变换是不改变秩的变换。

by 一万年太久只争朝夕 0 0
线性代数03-施光燕教授的笔记

逆矩阵慨念（相当于除法）：即矩阵的倒数。A-1=B,即AB=BA=I。主对角线，一个阵除了主对角线外，其余元素都为0,则为对角阵。对角阵的倒数，也就是逆矩阵，也是一个对角阵。矩阵乘法具有结合律，不改变次序。若n阶方阵A、B均可逆，则AB也可逆，且（AB）<-1>=B<-1>A<-1>.设A为n阶方阵，若A可逆，则A<-1>是唯一的。矩阵行列式 lA+Bl≠lAl+lBllλAl=λ<n>lAllABl=lAllBl，只有这个和行列式一样。可逆矩阵的判定定理：A可逆的充要条件为lAl≠0.矩阵运算和数的运算比较，有以下两点不同，其余均相同。不同处：AB不一定等于BAAB=0,不能推出A=0或B=0

by 一万年太久只争朝夕 1 1
线性代数02-施光燕教授的笔记

矩阵，A=B,[aij]mxn矩阵相加的前提是矩阵的规模相同。加法的交换律：A+B=B+A.零阵：O。A+O=A矩阵和数相乘还是一个矩阵。矩阵的减法。AB不一定等于BA。矩阵的乘法的前提的条件：当A的列数=B的行数。行阵、列阵、方阵、单位阵。IA=AI或EA=AE.矩阵的转置A',转置性质:(A+B)'=A'+B'(AB)'=B'A'如果A'=A，则称A为对称阵，对称阵为方阵。

by 一万年太久只争朝夕 1 1
线性代数01-施光燕教授的笔记

二阶行列式aij；三阶行列式；其中的每一个叫做元素。四阶行列式。一个元素的余子式（M11）；代数余子式A11。性质：1、行列交换，其值不变。2、两行交换，其值变号。3、若某一行有公因子，则可提出。4、对行的倍加运算，其值不变。

by 一万年太久只争朝夕 1 1
线性代数01-施光燕教授的笔记

行列式概念

by 月上清泉 0 0

你感兴趣的课程

开始学习

理学可汗学院公开课：概率

3万+浏览/ 247学员/ 4.6评分

免费

开始学习

国内大学高等数学

3万+浏览/ 1103学员/ 4.5评分

免费

开始学习

理学可汗学院：脑筋急转弯

2万+浏览/ 876学员/ 4.3评分

免费

学员动态

每日迫害章鱼哥收藏了课程线性代数

翰灵加入课程线性代数

待尘归开始学习课时线性代数01-施光燕教授

ES1620743852 开始学习课时线性代数01-施光燕教授

ES1620743852 加入课程线性代数

课程最新笔记

线性代数10-施光燕教授的笔记
一、相似矩阵本讲所讲的均为方阵。A-方阵，P为同一阶的可逆方阵，A通过相似变换P<-1>AP=B,称A和B相似，记为A~B。定理，若A和B相似，则A,B具有相同的特征方程，也即有相同的特征值。二、矩阵的对角化A~λ（对角阵）结论：若A=PλP<-1>,则λ中对角元素λi必为A得特征值，P中得列向量pi必为A相应于λi的特征向量，反之亦然。结论：对称阵一定可以对角化。
线性代数09-施光燕教授的笔记
矩阵的特征值和特征向量和秩一样，是矩阵另外一个特征，但是针对于方阵。概念：对于方阵A，若有非零向量X和数λ使得AX=λX，则称数λ为A的特征值，称非零向量X为A相应于特征值λ的特征向量。结论 A-nxm设λ1，λ2，…λn为A的特征值，则λ1+λ2+…+λn=A的迹（矩阵的对角线元素之和叫做矩阵的迹）λ1λ2…λn=lAl相当于解一元二次方程得韦达定理。求法：1、lA-λil=0(i为单位阵)，解出λ，即为矩阵A的特征值。2、求齐次线性方程组(A-λi)x=0的基础解系，即为特征向量。
线性代数08-施光燕教授的笔记
线性方程组（三）线性方程组的理论，AX=B,(B≠0)为非齐次线性方程组，r(A)=r([AB])<n，n-r(A)个自由变量。解的性质1、若Y为AX=B的解，X是AX=0的解，则Y+X亦为AX=B的解。2、若Y1、Y2均为AX=B的解，则Y1-Y2亦为AX=0的解。齐次通解：对于AX=B，若AX=B的一个解Y和AX=0的基础解系X1,X2,…，Xk，k=n-r(A)，则AX=B的所有解即为X=Y+c1X1+c2X2+…+ckXk(其中c1,c2,…，ck为任意常数)步骤1、[A,B]转换为阶梯阵。2、确定自由变量。3、令所有自由变量为0，求得AX=B的一个特解Y。4、求出AX=0的基础解系。5、求通解。
线性代数07-施光燕教授的笔记
线性方程组（二）若有解，解是否是唯一的？r(A)=r([AB])=n 等价于解唯一；r(A)=r([AB])<n 等价于解不唯一；且有n-r(A)个自由变量。有解，不唯一，怎么掌握全体？AX=O齐次线性方程组A-mxn，r(A)<n有n-r(A)个自由变量。若X1,X2均为AX=O的解，则C1X1+C2X2(C1、C2为任意常数)也是AX=O的解，{XlAX=O}（注意这是一个集合）中极大无关组，又称AX=O的基础解系。求AX=O齐次方程组的通解的步骤：1、化为阶梯阵。2、确定n-r(A)个自由变量。3、令一个自由变量为1，其它为0，用遍这样的办法，得到n-r（A）组解，即构成基础解析。4、基础解系中的解分别乘上任意常数相加，即得通解。